IPG

An Integer Programming Game is a simultaneous game among \(n\) players solving a parameterized (mixed) Integer Program. In ZERO, we support IPGs where each player \(i\) solves the following problem:

\[\begin{split}\min_{x^i} (c^i) ^\top x^i + (x^{-i})^\top C^ix^i + d^T x^{-i} \\ \text{s.t.} \quad A^ix^i\le b^i \\ \quad \quad x^i \ge 0 \\ \quad \quad x^i_j \in \mathbb{N} \quad \forall j \in \mathcal{I}^i\end{split}\]

Where \(\mathcal{I}\) is the set of indices of integer variables. In other words, the objective function takes a specific bi-linear form.

A quick example

Consider the following Integer Programming Game: The first player is the x player, whose decision variables are \(x\). The second player is the y player where its variables are \(y\).

Note

We slightly change the notation with respect to ZERO’s arguments for the exposition of this game. For instance, here for \(x\), we point to the first player’s variables instead of the parameters of a IP_Param. The example below should clarify any doubt.

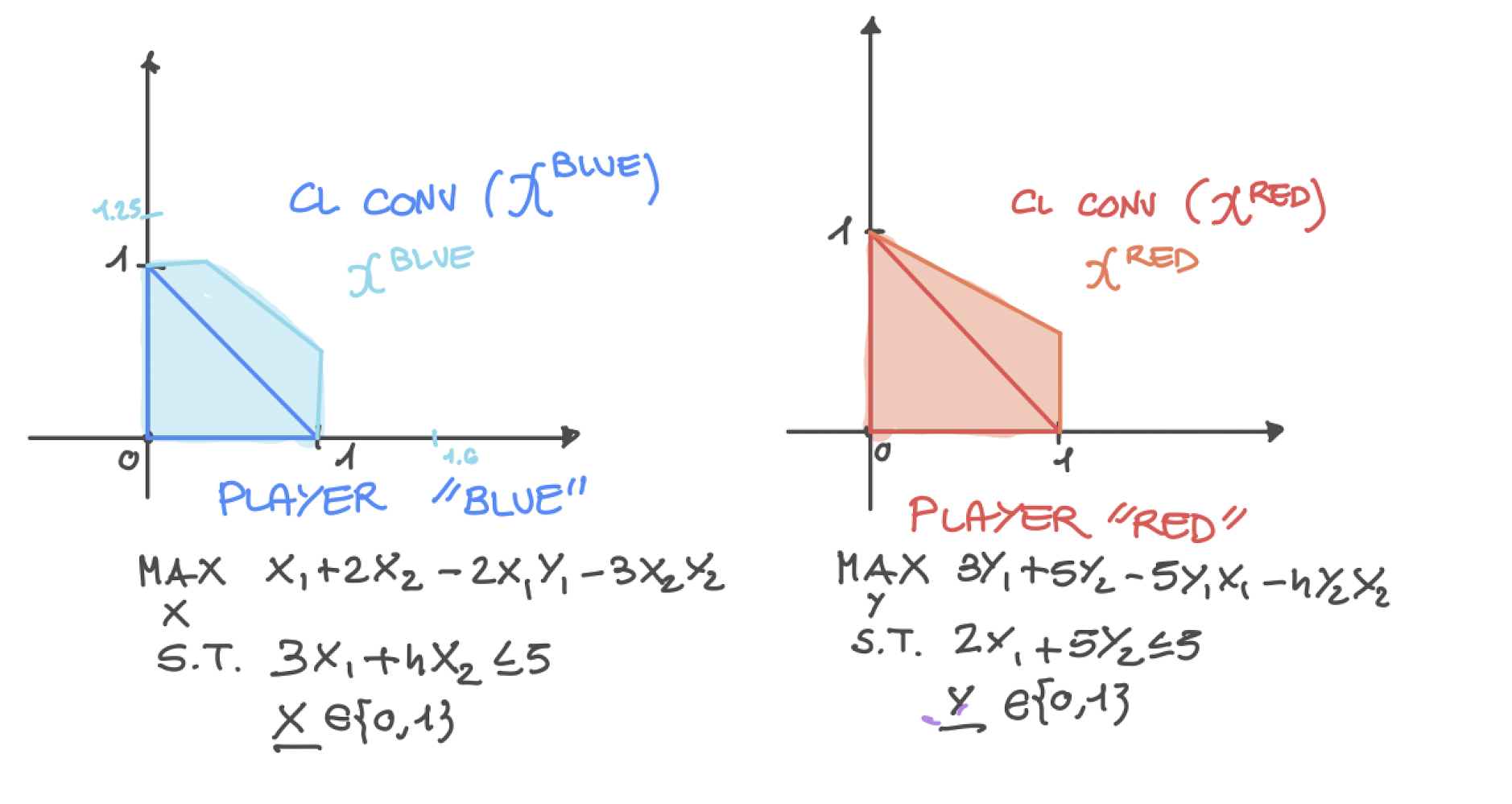
The Integer Programming Game for this example is a Knapsack Game.

The x player’s optimization problem is as follows

\[ \begin{align}\begin{aligned}\max_{x_1, x_2} x_1 + 2x_2 - 2x_1y_1 -3x_2y_2\\\text{s.t.} \quad 3x_1+4x_2 &\le 5\\\quad \quad x_1, x_2 &\in \{0,1\}\end{aligned}\end{align} \]

While the y player’s optimization problem is:

\[ \begin{align}\begin{aligned}\max_{y_1, y_2} 3y_1 + 5y_2 - 5y_1x_1 -4y_2x_2\\\text{s.t.} \quad 2y_1+5y_2 &\le 5\\\quad \quad y_1, y_2 &\in \{0,1\}\end{aligned}\end{align} \]

The problem has two pure Nash equilibria \((x_1, x_2, y_1, y_2) = (0, 1, 1, 0)\), and \((x_1, x_2, y_1, y_2) = (1, 0, 0, 1)\), and a mixed Equilibrium \((x_1, x_2, y_1, y_2) = (2/9, 7/9, 2/5, 3/5)\).

Modeling and solving the problem

The first step in modeling this Integer Programming Game is to include zero.h and create a derived class of Game::IPG. The minimal constructor for Game::IPG involves passing a pointer to GRBEnv (Check Gurobi’s C++ reference manual ). The derived class should indeed instantiate the base class (Game::IPG) using such a constructor. The code below gives an example.

#include <zero.h>


int main(int argc, char **argv) {

  GRBEnv GurobiEnv;
  try {

     Models::IPG::IPGInstance IPG_Instance; // The IPG Instance
     int                      numItems = 2, numPlayers = 2;

     arma::vec      c(numItems), d(numItems * (numPlayers - 1));                              // Profits c in the objective
     arma::sp_mat   C(numItems * (numPlayers - 1), numItems); // C terms in the objective
     arma::sp_mat   a(1, numItems);                           // LHS for Knapsack constraint
     arma::vec      b(1);                                     // RHS for constraints
     arma::vec      IntegerIndexes(numItems);                 // The index of the integer variables
     VariableBounds VarBounds = {{0, 1}, {0, 1}};             // Implicit bounds on variables

     // Fill the values in the paramterized integer problem
     for (unsigned int i = 0; i < numItems; ++i)
        IntegerIndexes.at(i) = i;

     C(0, 0) = 2; // C terms in the objective
     C(1, 1) = 3;
     a(0, 0) = 3; // Knapsack Constraints
     a(0, 1) = 4;
     b(0)    = 5;  // Knapsack Capacity
     c(0)    = -1; // The standard is minimization, hence minus
     c(1)    = -2;
     d(0)    = 0;
     d(1)    = 0;

     // Create a parametrized Integer Program
     MathOpt::IP_Param PlayerOne(C, a, b, c, d, IntegerIndexes, VarBounds, &GurobiEnv);

     // Parametrized Integer Program for the second player.
     C(0, 0) = 5;
     C(1, 1) = 4;
     a(0, 0) = 2;
     a(0, 1) = 5;
     c(0)    = -3;
     c(1)    = -5;

     MathOpt::IP_Param PlayerTwo(C, a, b, c, d, IntegerIndexes, VarBounds, &GurobiEnv);

     // Add the players to the instance. We can also specify a file path to write the instance
     IPG_Instance.addIPParam(PlayerOne, "A_Parametrized_KnapsackProblem1");
     IPG_Instance.addIPParam(PlayerTwo, "A_Parametrized_KnapsackProblem2");
     IPG_Instance.save("A_Knapsack_Game"); // Save the instance with the standardize format
     Models::IPG::IPG KnapsackGame(&GurobiEnv, IPG_Instance); // Create a model from the instance
     // A few optional settings
     KnapsackGame.setNumThreads(4);            // How many threads, if supported by the solver?
     KnapsackGame.setTimeLimit(5);             // Time limit in second
     KnapsackGame.finalize();                  // Lock the model
     KnapsackGame.setDeviationTolerance(3e-4); // Numerical tolerance
     // Run and get the results


     // Cut and Play
     KnapsackGame.setAlgorithm(Data::IPG::Algorithms::CutAndPlay);
     KnapsackGame.setLCPAlgorithm(Data::LCP::Algorithms::MIP); // How do we solve the LCPs?
     KnapsackGame.findNashEq();
     std::cout << "The Cut-and-Play solution" << std::endl;
     KnapsackGame.getX().at(0).print("Player 1:"); // Print the solution
     KnapsackGame.getX().at(1).print("\n Player 2:");

     // Zero Regrets
     KnapsackGame.setAlgorithm(Data::IPG::Algorithms::ZERORegrets);
     KnapsackGame.setGameObjective(Data::IPG::Objectives::ZERORegrets_PlayerOne);
     KnapsackGame.findNashEq();
     std::cout << "The ZERO Regrets solution" << std::endl;
     KnapsackGame.getX().at(0).print("Player 1:"); // Print the solution
     KnapsackGame.getX().at(1).print("\n Player 2:");
  } catch (ZEROException &e) {
     throw ZEROException(e);
  }
}