Class NashGame

Defined in File nash.h

Class Documentation

class NashGame

Class to model Nash-cournot games with each player playing a QP.

Stores a vector of QPs with each player’s optimization problem. Potentially common (leader) constraints can be stored too.

Helpful in rewriting the Nash-Cournot game as an LCP Helpful in rewriting leader constraints after incorporating dual variables etc

Warning

This has public fields which if accessed and changed can cause undefined behavior!

Public Functions

inline explicit NashGame(GRBEnv *e) noexcept: To be used only when NashGame is being loaded from a file.

explicit NashGame(GRBEnv *e, const std::vector<std::shared_ptr<MathOpt::MP_Param>> &players, arma::sp_mat MC, arma::vec MCRHS, unsigned int nLeadVar = 0, arma::sp_mat leadA = {}, arma::vec leadRHS = {})

Constructing a NashGame from a set of MathOpt::MP_Param, Market clearing constraints.

Construct a NashGame by giving a std::vector of pointers to MP_Param, defining each player’s game A set of Market clearing constraints and its RHS And if there are leader variables, the number of leader vars.

Have a std::vector of pointers to MathOpt::MP_Param ready such that the variables are separated in \(x^{i}\) and \(x^{-i}\) format.

In the correct ordering of variables, have the Market clearing equations ready.

Now call this constructor. It will allocate appropriate space for the dual variables for each player.

Parameters

e – A pointer to the Gurobi Environment
players – The MathOpt::MP_Param associated to the players
MC – Market clearing LHS matrix
MCRHS – Market clearing RHS vector
nLeadVar – Number of leaders’ variables
leadA – Leaders’ constraints
leadRHS – Leaders’ RHSs

NashGame(const NashGame &N)

Default copy constructor.

Parameters: N – The original copy object

~NashGame() = default: Default destructor.

inline unsigned int getNprimals() const: Read-only access to the number of of primal variables.

inline unsigned int getNumShadow() const: Read-only access to the number of Market clearing Shadow prices, equal to the number of Market clearing constraints.

inline unsigned int getNumLeaderVars() const: Read-only access to the number of the leader variables in the problem.

inline unsigned int getNumDualVars() const: Read-only access to the number of dual variables and that is indeed the sum of the number dual variables for each player.

inline unsigned int getPrimalLoc(unsigned int i = 0) const: Read-only access to the primal variable of i th player.

inline unsigned int getMCDualLoc() const: Read-only access to the Market-clearing dual variables start position.

inline unsigned int getLeaderLoc() const: Read-only access to the leaders’ variables start position.

inline unsigned int getDualLoc(unsigned int i = 0) const: Read-only access to the dual variables start position.

const NashGame &formulateLCP(arma::sp_mat &M, arma::vec &q, perps &Compl, VariableBounds &Bounds, bool writeToFile = false, const std::string &M_name = "dat/LCP.txt", const std::string &q_name = "dat/q.txt") const

Formulates the LCP corresponding to the Nash game. Computes the KKT conditions for each Player, calling MP_Param::KKT. Arranges them systematically to return M, q as an LCP \(0\leq q \perp Mx+q \geq 0 \). The way the variables of the players get distributed is shown in the image below.

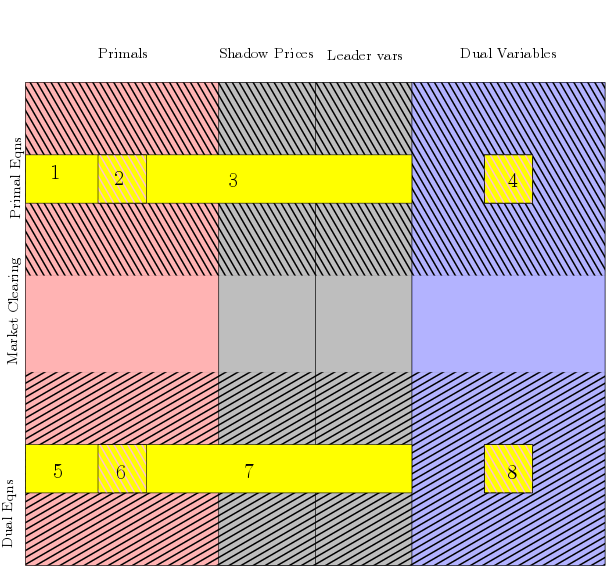
../_images/FormulateLCP.png

Warning

Does not return the leader constraints. Use NashGame::rewriteLeadCons() to handle them

Parameters

M – The output matrix M
q – The output vector q
Compl – The output complementarities pairings
OutBounds – The output Bounds on variables
writeToFile – If true, writes M and q to file.k
M_name – Filename for M
q_name – Filename for Q

Returns

arma::sp_mat rewriteLeadCons() const

Rewrites leader constraint adjusting for dual variables. Rewrites leader constraints given earlier with added empty columns and spaces corresponding to Market clearing duals and other equation duals. This becomes important if the Lower level complementarity problem is passed to LCP with upper level constraints.

Returns: The matrix with the leader constraints

inline arma::vec getLeadRHS() const

Gets the RHS of the Leader Constraints.

Returns: THe LeaderConstraintsRHS object

inline arma::vec getMCLeadRHS() const

Gets the RHS of the Market Clearing Constraints plus the leader ones.

Returns: THe queried object

std::unique_ptr<GRBModel> respond(unsigned int player, const arma::vec &x, bool fullvec = true) const

Given the decision of other players, find the optimal response for player in position player. Given the strategy of each player, returns a Gurobi Model that has the optimal strategy of the player at position player.

Parameters

player – The player id
x – A std::vector of pure strategies (either for all players or all other players)
fullvec – True if x contains the strategy for all players

Returns

double respondSol(arma::vec &sol, unsigned int player, const arma::vec &x, bool fullvec = true) const

Returns the optimal objective value that is obtainable for the player player given the decision x of all other players. Calls Game::NashGame::respond and obtains the std::unique_ptr to GRBModel of best response by player player. Then solves the model and returns the appropriate objective value.

Parameters

sol – Output optimal response
player – The input player’s id
x – A std::vector of pure strategies (either for all players or all other players)
fullvec – True if x contains the strategy for all players

Returns

The optimal objective value for the player player.

arma::vec computeQPObjectiveValues(const arma::vec &x, bool checkFeas = false) const

Computes players’ objective. Computes the objective value of each player in the Game::NashGame object.

Returns: An arma::vec with the objective values.

bool isSolved(const arma::vec &sol, unsigned int &violPlayer, arma::vec &violSol, double tol = 1e-4) const

Checks if the Nash game is solved.

Checks if the Nash game is solved, if not provides a proof of deviation

Parameters

sol – The std::vector of pure strategies for the Nash Game
violPlayer – Output index of the player with profitable deviation
violSol – The output pure strategy for that player - which gives a profitable deviation
tol – The deviation tolerance

NashGame &addDummy(unsigned int par = 0, int position = -1)

Add dummy variables (parameters) in a NashGame object. These are just zero columns that don’t feature in the problem anywhere. They are of importance only where the NashGame gets converted into an LCP and gets parametrized. Typically, they appear in the upper level objective in such a case.

Parameters

par – Number of parameters
position – Position of the parameters

Returns

NashGame &addLeadCons(const arma::vec &a, double b)

Adds Leader constraint to a NashGame object. In case common constraint to all followers is to be added (like a leader constraint in an MPEC), this function can be used. It adds a single constraint \( a^Tx \leq b\).

Parameters

a – The constraint LHS
b – The constraint RHS

Returns

A pointer to this

void write(const std::string &filename, bool append = true, bool KKT = false) const

Writes the Nash Game sum up to a file.

Parameters

filename – The filename
append – Should the method append to the file?
KKT – True if the KKT needs to be included

void save(const std::string &filename, bool erase = true) const: Saves the Game::NashGame object in a loadable file.

long int load(const std::string &filename, long int pos = 0)

Loads the Game::NashGame object stored in a file.

Loads the NashGame object stored in a file. Before calling this function, use the constructor NashGame::NashGame(GRBEnv *Env) to initialize. Loads the NashGame object stored in a file. Before calling this function, use the constructor NashGame::NashGame(GRBEnv *Env) to initialize.

Example usage:

int main()
{
        GRBEnv Env;
        Game::NashGame N(&Env);
        N.load("./dat/Ndata.dat");
        std::cout<<N<<'\n';
        return 0;
}

Parameters

filename – The filename
pos – The start writing position

Returns

The end position

Private Functions

void setPositions()

Stores the position of each players’ primal and dual variables. Also allocates Leader’s position appropriately. The ordering is according to the columns of the following image.

../_images/FormulateLCP.png

Private Members

GRBEnv *Env = nullptr: A pointer to the Gurobi Environment.

arma::sp_mat LeaderConstraints: Upper level leader constraints LHS.

arma::vec LeaderConstraintsRHS: Upper level leader constraints RHS.

unsigned int NumPlayers: Number of players in the Nash Game.

VariableBounds Bounds: BoundsX on primal variables.

std::vector<std::shared_ptr<MathOpt::MP_Param>> Players: The QP that each player solves.

arma::sp_mat MarketClearing: Market clearing constraints.

arma::vec MCRHS: RHS to the Market Clearing constraints.

std::vector<unsigned int> PrimalPosition: In the vector of variables of all players, which position does the variable corresponding to this player starts.

std::vector<unsigned int> DualPosition: In the vector of variables of all players, which position do the DUAL variable corresponding to this player starts.

unsigned int MC_DualPosition = {}: Manages the position of Market clearing constraints’ duals.

unsigned int LeaderPosition = {}: Manages the position of where the leader’s variables start.

unsigned int numLeaderVar: Manages the position of where the leader’s variables start. These many variables will not have a matching complementary equations.

Friends

inline friend std::ostream &operator<<(std::ostream &os, const NashGame &N)