Game

namespace Game

This namespace contains the definitions for classes related to games.

class EPEC : public Game::AbstractGame<Data::EPEC::DataObject>

#include <epec.h>

Class to handle a Nash game between leaders of Stackelberg games.

Subclassed by Models::EPEC::EPEC

Public Functions

inline EPEC(GRBEnv *env)

The standard constructor. Initialize an empty instance.

Parameters

env – The Gurobi environment pointer.

void finalize()

Finalizes the creation of a Game::EPEC object.

Performs a bunch of job after all data for a Game::EPEC object are given, namely. Models::EPEC::computeLeaderLocations - Adds the required dummy variables to each leader’s problem so that a game among the leaders can be defined. Calls Game::EPEC::addDummyLead

• Makes the market clearing constraint in each country. Calls

virtual void findNashEq() override

Computes Nash equilibrium using the Algorithm set in Game::EPEC::Algorithm. Checks the value of Game::EPEC::Algorithm and delegates the task to appropriate Algorithm wrappers.

virtual bool isSolved(double tol = 1e-5) const override

Call the delegated Algorithm method and return true if there exist a feasible equilibrium.

Parameters

tol – A numerical tolerance

Returns

True if the incumbent solution is an equilibrium

virtual bool isPureStrategy(double tol = 1e-5) const override

Call the delegated Algorithm method and return true if the equilibrium is pure.

Parameters

tol – A numerical tolerance

Returns

True if the incumbent equilibrium is pure

std::unique_ptr<GRBModel> bestResponseProgram(const unsigned int i, const arma::vec &x, MathOpt::PolyLCP *customLCP = nullptr) const

Given a player id i, the incumbent solution x (and optionally a custom player LCP customLCP), this method returns the model corresponding to the best response of i given the other players’ decisions in x.

Parameters

• i – The player id

• x – The incumbent solution

• customLCP – An optional parameter with a custom LCP

Returns

A pointer to the (solved) Gurobi model for the best response

double bestResponse(arma::vec &sol, unsigned int player, const arma::vec &x, const arma::vec &prevDev = {}, MathOpt::PolyLCP *customLCP = nullptr) const

Returns the best-response value for the player player given the decision x of all other players.

Calls Game::EPEC::respond and obtains the std::unique_ptr to GRBModel of best response by player player. Then solves the model and returns the appropriate objective value.

Parameters

• sol – The optimal response for player

• player – The player id

• x – The solution vector

• prevDev – An optional previous deviation encountered. This is useful to normalize any unbounded best response

• customLCP – An optional pointer to a custom player LCP.

Returns

The optimal objective value for the player player.

inline const arma::vec getX() const

Getter for the incumbent solution (x)

Returns

The incumbent x

inline const arma::vec getZ() const

Getter for the incumbent solution (z)

Returns

The incumbent z

void setAlgorithm(Data::EPEC::Algorithms algorithm)

Decides the Algorithm to be used for solving the given instance of the problem. The choice of algorithms are documented in Game::EPECalgorithm.

Parameters

algorithm – The input algorithm

void setRecoverStrategy(Data::EPEC::RecoverStrategy strategy)

Decides the Algorithm to be used for recovering a PNE out of the InnerApproximation procedure.

Parameters

strategy – Input ecovery strategy

void setBranchingStrategy(Data::EPEC::BranchingStrategy strategy)

Sets the branching strategy for the CutAndPlay.

Parameters

strategy – The input strategy

inline void setAggressiveness(unsigned int a)

inline void setAddPolyMethod(Data::LCP::PolyhedraStrategy add)

Set the Data::LCP::PolyhedraStrategy for the inner approximation.

unsigned int getPositionLeadFoll(unsigned int i, unsigned int j) const

Gets the position of the j-th variable in the i-th leader Querying Game::EPEC::LCPModel for x[return-value] variable gives the appropriate variable.

Parameters

• i – Leader number

• j – Follower number

Returns

The queried position

unsigned int getPositionLeadLead(unsigned int i, unsigned int j) const

Gets the position of the j-th Follower variable in the i-th leader Querying Game::EPEC::LCPModel for x[return-value] variable gives the appropriate variable.

Parameters

• i – Leader number

• j – Follower number

Returns

The queried position

double getValLeadFoll(unsigned int i, unsigned int j) const

Gets the value of the j-th variable in i-th leader.

Parameters

• i – Leader number

• j – Follower number

Returns

The queried position

double getValLeadLead(unsigned int i, unsigned int j) const

Gets the value of the j-th non-follower variable in i-th leader.

Parameters

• i – Leader number

• j – Follower number

Returns

The queried position

double getValProbab(unsigned int i, unsigned int k)

Returns the probability associated with the k -th polyhedron of the i -th leader.

Parameters

• i – Leader index

• k – The polyhedron index

Returns

The queried attribute

double getValLeadFollPoly(unsigned int i, unsigned int j, unsigned int k, double tol = 1e-5) const

For the i -th leader, gets the k -th pure strategy at position j.

Parameters

• i – The leader index

• j – The position index

• k – The pure strategy index

• tol – A numerical tolerance

Returns

The queried attribute

double getValLeadLeadPoly(unsigned int i, unsigned int j, unsigned int k, double tol = 1e-5) const

For the i -th leader, gets the k -th pure strategy at leader position j.

Parameters

• i – The leader index

• j – The position index

• k – The pure strategy index

• tol – A numerical tolerance

Returns

The queried attribute

std::vector<unsigned int> mixedStrategyPoly(unsigned int i, double tol = 1e-5) const

Returns the indices of polyhedra feasible for the leader, from which strategies are played with probability greater than the tolerance.

Parameters

• i – Leader index

• tol – Tolerance

Returns

The queried attribute

inline const MathOpt::LCP &getLCPDescription() const

Get the Game::LCP object solved in the last iteration either to solve the problem or to prove non-existence of Nash equilibrium. Object is returned using constant reference.

inline const GRBModel &getLCPModel() const

Get the GRBModel solved in the last iteration to solve the problem or to prove non-existence of Nash equilibrium. Object is returned using constant reference.

inline void writeLCPModel(const std::string &filename) const

Writes the GRBModel solved in the last iteration to solve the problem or to prove non-existence of Nash equilibrium to a file.

void getXWithoutHull(const arma::vec &x, arma::vec &xWithoutHull) const

Given the the solution x, the method returns in xWithoutHull the x vector without the convex-hull’s variables. Also, no MC variables are included.

Parameters

• x – The EPEC’s solution

• xWithoutHull – The output solution without convex hull variables

void getXofI(const arma::vec &x, const unsigned int &i, arma::vec &xOfI, bool hull = false) const

Given the player id i and the solution x, the method returns in xWithoutHull the x vector for the given player, with the convex-hull’s variables in case hull is false. Also, no MC variables are included.

Parameters

• x – The EPEC’s solution

• i – The player id

• xOfI – Output solution vector for i

• hull – True if convex-hull variables need to be included in the output

void setWelfareObjective(bool linear, bool quadratic)

Given the object Game::EPEC::LCPModel, this method sets its objective to the social welfare. In specific, we can decide whether to include or not the linear or quadratic part of the welfare

Parameters

• linear – True if the linear part is to be included, false otherwise.

• quadratic – True if the quadratic part is to be included, false otherwise.

Protected Functions

bool warmstart(const arma::vec &x)

Warmstarts EPEC with a solution.

Warmstart the solution with x.

Todo:

Complete this implementation

Parameters

x – The warmstart solution

Returns

True if the warmstart was successful

virtual void makeObjectivePlayer(const unsigned int i, MathOpt::QP_Objective &QP_obj) = 0

Empty function - optionally re-implementable in derived class.

Parameters

• i – The player id

• QP_obj – The QP_object with the objective

virtual void preFinalize() = 0

Empty function - optionally re-implementable in derived class.

This function can be optionally implemented by the derived class. Code in this class will be run before calling Game::EPEC::finalize().

virtual void postFinalize() = 0

Empty function - optionally re-implementable in derived class.

This function can be optionally implemented by the derived class. Code in this class will be run after calling Game::EPEC::finalize().

virtual void updateLocations() = 0

Empty function - optionally re-implementable in derived class.

If any location tracking system is implemented, that can be called from in here.

inline virtual void makeMCConstraints(arma::sp_mat &MC, arma::vec &RHS) const

Empty function - optionally re-implementable in derived class.

Builds the Market Clearing constraints

Parameters

• MC – MC constraints matrix

• RHS – RHS for the constraints

Protected Attributes

std::vector<std::shared_ptr<Game::NashGame>> PlayersLowerLevels = {}

The lower level Nash Games among the followers.

std::vector<std::shared_ptr<MathOpt::LCP>> PlayersLCP = {}

The LCP of each leader, encompassing both Stackelberg and low-level Nash games.

std::vector<std::shared_ptr<MathOpt::QP_Param>> PlayersQP = {}

The QP corresponding to each player.

std::vector<std::shared_ptr<MathOpt::QP_Objective>> LeaderObjective = {}

Objective of each leader.

std::vector<std::shared_ptr<MathOpt::QP_Objective>> LeaderObjectiveConvexHull = {}

Objective of each leader, given the convex hull computation.

std::unique_ptr<Game::NashGame> TheNashGame

The EPEC nash game.

std::vector<unsigned int> LeaderLocations = {}

Location of each leader Number of variables in the current player, including any number of convex hull variables at the current moment. The used, i.e., the inheritor of Game::EPEC has the responsibility to keep this correct by implementing an override of Game::EPEC::updateLocations.

std::vector<const unsigned int*> LocEnds = {}

The ending locations for the leaders’ variables.

std::vector<unsigned int> ConvexHullVariables = {}

Number of convex hull variables for each leader.

unsigned int numMCVariables = {0}

Number of market clearning variables.

bool Finalized = {false}

A flag controlling if the EPEC was finalized.

arma::vec SolutionZ

Solution equation values.

arma::vec SolutionX

Solution variable values.

Private Functions

void addDummyLead(unsigned int i)

Add Dummy variables for the leaders.

Adds dummy variables to the leader of an EPEC - useful after computing the convex hull.

Parameters

i – The leader id to whom dummy variables should be added

void makePlayerQP(unsigned int i)

Makes the MathOpt::QP_Param corresponding to the i-th country.

• First gets the Game::LCP object from Game::EPEC::PlayersLowerLevels and makes a MathOpt::QP_Param with this LCP as the lower level

• This is achieved by calling LCP::makeQP and using the objective value object in Game::EPEC::LeaderObjective

• Finally the locations are updated owing to the complete convex hull calculated during the call to LCP::makeQP

Note

Overloaded as Models::EPEC::makePlayerQP()

Parameters

i – The player’s id

void makePlayersQPs()

Makes the MathOpt::QP_Param for all the countries. Calls are made to Models::EPEC::makePlayerQP(const unsigned int i) for each valid player id.

void makeTheLCP()

Formulates the LCP to compute an equilibrium. In this LCP, each player’s feasible region is given by the PlayersQP associated entry. If the QP stems from a full enumeration, for instance, the solution will be exact.

void computeLeaderLocations(unsigned int addSpaceForMC = 0)

Assigns the values to LeaderLocations to each player.

Parameters

addSpaceForMC – contains the number of Market Clearing variables

void getXMinusI(const arma::vec &x, const unsigned int &i, arma::vec &xMinusI) const

Given a solution in x, computes the other players’ solution x minus i in xMinusI.

Parameters

• x – The incumbent solution

• i – The player id

• xMinusI – The output strategy

bool computeNashEq(bool pureNE, double localTimeLimit, bool check, bool linearWelfare, bool quadraticWelfare)

Given that Game::EPEC::PlayersQP are all filled with a each country’s MathOpt::QP_Param problem (either exact or approximate), computes the Nash equilibrium. pureNE checks for pure Nash Equilibrium. It does not work with EPEC::Algorithms::CutAndPlay localTimeLimit sets the timelimit for the solver. a negative value is infinite time check If true, the method calls the isSolved() method related to the active algorithm EPEC::Algorithms linearWelfare If true, the objective of the resulting LCP includes the sum of the linear objectives for the players quadraticWelfare If true, the objective of the resulting LCP includes the sum of the quadratic objectives for the players

Returns

true if a Nash equilibrium is found

Private Members

std::shared_ptr<Algorithms::EPEC::PolyBase> Algorithm = {}

The incumbent algorithm used to solve the instance.

std::vector<unsigned int> SizesWithoutHull = {}

Size of leaders’ variables without the convex hull variables.

std::unique_ptr<MathOpt::LCP> TheLCP

The EPEC nash game written as an LCP.

std::unique_ptr<GRBModel> LCPModel

A Gurobi mode object of the LCP form of EPEC.

std::unique_ptr<GRBModel> LCPModelBase

A Gurobi mode object of the LCP form of EPEC. If we are searching for a pure NE, the LCP which is indifferent to pure or mixed NE is stored in this object.

Friends

friend class Algorithms::EPEC::PolyBase

friend class Algorithms::EPEC::InnerApproximation

friend class Algorithms::EPEC::CutAndPlay

friend class Algorithms::EPEC::CombinatorialPNE

friend class Algorithms::EPEC::FullEnumeration

template<typename DataObjectType>
class AbstractGame

#include <games.h>

An abstract class for a game.

Template Parameters

DataObjectType – The object type for the data

class aGame : public AbstractGame<Data::aGame::DataObject>{

   public:
     //Override AbstractGame methods
    void findNashEq() override;
    bool       isSolved(double tol = 1e-5) const override;
    bool isPureStrategy(double tol = 1e-5) const override;

}

Public Functions

inline AbstractGame(GRBEnv *env)

Standard constructor with the Gurobi Environment.

Parameters

env – A pointer to the Gurobi environment

AbstractGame() = default

Default constructor.

AbstractGame(AbstractGame&) = delete

Copy constructor. Not active.

~AbstractGame() = default

Deconstructor.

virtual void findNashEq() = 0

The main method to start the solving process.

virtual bool isSolved(double tol = 1e-5) const = 0

Return a bool true if the strategies are all pure, for any player.

virtual bool isPureStrategy(double tol = 1e-5) const = 0

Return a bool indicating whether the equilibrium is a pure strategy.

inline ZEROStatistics<DataObjectType> getStatistics() const

Getter for statistics.

Returns

Returns the appropriate Data Object Type

inline void setNumThreads(unsigned int t)

Sets the number of threads for Gurobi.

Parameters

t – The number of threads

inline void setRandomSeed(unsigned int t)

Sets the random seed for pseudo-random operations.

Parameters

t – The seed

inline void setPureNashEquilibrium(bool val)

Requires the algorithm to find a pure equilibrium.

Warning

This field may not be used by all the inheritor algorithms.

Parameters

val – The boolean requirement

inline void setDeviationTolerance(double val)

Sets the tolerance for profitable deviations.

Parameters

val – Deviation tolerance

inline void setTimeLimit(double val)

Sets the timelimit.

Parameters

val – The timelimit

inline int getNumVar() const noexcept

Gets the number of variables.

Returns

The number of variable

inline int getNumPlayers() const noexcept

Gets the number of players.

Returns

The number of players

Protected Attributes

std::chrono::high_resolution_clock::time_point InitTime

ZEROStatistics<DataObjectType> Stats = ZEROStatistics<DataObjectType>(DataObjectType())

GRBEnv *Env = {}

Store run time information.

The Gurobi environment

unsigned int NumVariables = {0}

The number of variables in the game.

unsigned int NumPlayers = {0}

The number of players in the game.

bool NashEquilibrium = {false}

True if computeNashEq returned an equilibrium. Note that this can be the equilibrium of an approximation, and not to the original game. Refer to isSolved() to get a definitive answer.

class IPG : public Game::AbstractGame<Data::IPG::DataObject>

#include <ipg.h>

This class handles Integer Programming Games (IPG), namely multiple agents solving an integer programming game.

Subclassed by Models::IPG::IPG

Public Functions

void finalize()

This methods finalizes the model by disabling any edits to the number of players. The proper object (for instance, the ones counting players variables) are initialized with the right values.

inline IPG(GRBEnv *env)

Standard initializer.

Parameters

env – A pointer to the Gurobi Environment

IPG(GRBEnv *env, std::vector<std::shared_ptr<MathOpt::IP_Param>> players)

This constructors initializes the integer programming game with the Gurobi environment env and the vector of shared pointers to the IP_Params in players.

Parameters

• env – A pointer to the Gurobi Environment

• players – A vector containing the pointers to the IP param for each player

• env – Pointer to the Gurobi environment

• players – The MathOpt::IP_Param for the players

virtual void findNashEq() override

The main method to start the solving process.

virtual bool isSolved(double tol = 1e-5) const override

Return a bool true if the strategies are all pure, for any player.

virtual bool isPureStrategy(double tol = 1e-5) const override

Return a bool indicating whether the equilibrium is a pure strategy.

inline std::vector<arma::vec> getX() const

Gets the X in the incumbent solution.

Returns

A const vector copy of X.

inline double getSocialWelfare() const

inline ZEROStatistics<Data::IPG::DataObject> getStatistics() const

Get the EPECStatistics object for the current instance.

inline void setAlgorithm(Data::IPG::Algorithms algorithm)

Sets the Data::IPG::Algorithms for the solution process.

Parameters

algorithm – An enum from Data::IPG::Algorithms

inline void setPresolve(bool value)

Sets the Data::IPG::Presolve for the solution process.

Parameters

value – A boolean for Data::IPG::Presolve

inline void setLCPAlgorithm(const Data::LCP::Algorithms algo)

Sets the Data::LCP::Algorithms for the LCP solution process.

Parameters

algo – An enum from Data::LCP::Algorithms

inline void setGameObjective(const Data::IPG::Objectives obj)

Sets the Data::IPG::Objectives for the LCP objective.

Parameters

obj – An enum from Data::IPG::Objectives

inline void setCutsAggressiveness(const Data::IPG::CutsAggressiveness aggressiveness)

Sets the Data::IPG::CutsAggressiveness for the cut aggressiveness in Algorithms::IPG::CutAndPlay.

Parameters

aggressiveness – An enum from Data::IPG::CutsAggressiveness

Protected Functions

virtual void preFinalize() = 0

Virtual (empty) method. Can be implemented by a derived class.

virtual void postFinalize() = 0

Virtual (empty) method. Can be implemented by a derived class.

Protected Attributes

std::vector<std::shared_ptr<MathOpt::IP_Param>> PlayersIP = {}

The Integer Programs associated to each player.

std::vector<unsigned int> PlayerVariables = {}

The number of variables for each player.

bool Finalized = {false}

std::vector<arma::vec> Solution

Solution variable values, for each player.

double SocialWelfare

SocialWelfare associated to the incumbent solution.

Private Members

std::shared_ptr<Algorithms::IPG::Algorithm> Algorithm = {}

The Algorithm’s instance.

Friends

friend class Algorithms::IPG::Algorithm

friend class Algorithms::IPG::CutAndPlay

friend class Algorithms::IPG::ZERORegrets

class NashGame

#include <nash.h>

Class to model Nash-cournot games with each player playing a QP.

Stores a vector of QPs with each player’s optimization problem. Potentially common (leader) constraints can be stored too.

Helpful in rewriting the Nash-Cournot game as an LCP Helpful in rewriting leader constraints after incorporating dual variables etc

Warning

This has public fields which if accessed and changed can cause undefined behavior!

Public Functions

inline explicit NashGame(GRBEnv *e) noexcept

To be used only when NashGame is being loaded from a file.

explicit NashGame(GRBEnv *e, const std::vector<std::shared_ptr<MathOpt::MP_Param>> &players, arma::sp_mat MC, arma::vec MCRHS, unsigned int nLeadVar = 0, arma::sp_mat leadA = {}, arma::vec leadRHS = {})

Constructing a NashGame from a set of MathOpt::MP_Param, Market clearing constraints.

Construct a NashGame by giving a std::vector of pointers to MP_Param, defining each player’s game A set of Market clearing constraints and its RHS And if there are leader variables, the number of leader vars.

Have a std::vector of pointers to MathOpt::MP_Param ready such that the variables are separated in \(x^{i}\) and \(x^{-i}\) format.

In the correct ordering of variables, have the Market clearing equations ready.

Now call this constructor. It will allocate appropriate space for the dual variables for each player.

Parameters

• e – A pointer to the Gurobi Environment

• players – The MathOpt::MP_Param associated to the players

• MC – Market clearing LHS matrix

• MCRHS – Market clearing RHS vector

• nLeadVar – Number of leaders’ variables

• leadA – Leaders’ constraints

• leadRHS – Leaders’ RHSs

NashGame(const NashGame &N)

Default copy constructor.

Parameters

N – The original copy object

~NashGame() = default

Default destructor.

inline unsigned int getNprimals() const

Read-only access to the number of of primal variables.

inline unsigned int getNumShadow() const

Read-only access to the number of Market clearing Shadow prices, equal to the number of Market clearing constraints.

inline unsigned int getNumLeaderVars() const

Read-only access to the number of the leader variables in the problem.

inline unsigned int getNumDualVars() const

Read-only access to the number of dual variables and that is indeed the sum of the number dual variables for each player.

inline unsigned int getPrimalLoc(unsigned int i = 0) const

Read-only access to the primal variable of i th player.

inline unsigned int getMCDualLoc() const

Read-only access to the Market-clearing dual variables start position.

inline unsigned int getLeaderLoc() const

Read-only access to the leaders’ variables start position.

inline unsigned int getDualLoc(unsigned int i = 0) const

Read-only access to the dual variables start position.

const NashGame &formulateLCP(arma::sp_mat &M, arma::vec &q, perps &Compl, VariableBounds &Bounds, bool writeToFile = false, const std::string &M_name = "dat/LCP.txt", const std::string &q_name = "dat/q.txt") const

Formulates the LCP corresponding to the Nash game. Computes the KKT conditions for each Player, calling MP_Param::KKT. Arranges them systematically to return M, q as an LCP \(0\leq q \perp Mx+q \geq 0 \). The way the variables of the players get distributed is shown in the image below.

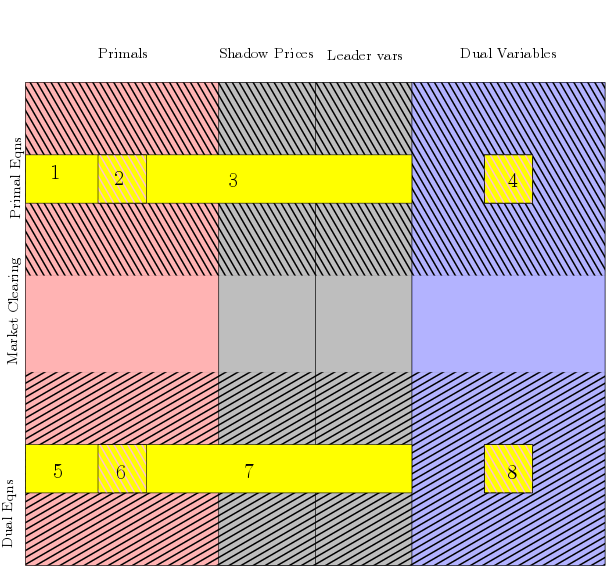
Warning

Does not return the leader constraints. Use NashGame::rewriteLeadCons() to handle them

Parameters

• M – The output matrix M

• q – The output vector q

• Compl – The output complementarities pairings

• OutBounds – The output Bounds on variables

• writeToFile – If true, writes M and q to file.k

• M_name – Filename for M

• q_name – Filename for Q

Returns

arma::sp_mat rewriteLeadCons() const

Rewrites leader constraint adjusting for dual variables. Rewrites leader constraints given earlier with added empty columns and spaces corresponding to Market clearing duals and other equation duals. This becomes important if the Lower level complementarity problem is passed to LCP with upper level constraints.

Returns

The matrix with the leader constraints

inline arma::vec getLeadRHS() const

Gets the RHS of the Leader Constraints.

Returns

THe LeaderConstraintsRHS object

inline arma::vec getMCLeadRHS() const

Gets the RHS of the Market Clearing Constraints plus the leader ones.

Returns

THe queried object

std::unique_ptr<GRBModel> respond(unsigned int player, const arma::vec &x, bool fullvec = true) const

Given the decision of other players, find the optimal response for player in position player. Given the strategy of each player, returns a Gurobi Model that has the optimal strategy of the player at position player.

Parameters

• player – The player id

• x – A std::vector of pure strategies (either for all players or all other players)

• fullvec – True if x contains the strategy for all players

Returns

double respondSol(arma::vec &sol, unsigned int player, const arma::vec &x, bool fullvec = true) const

Returns the optimal objective value that is obtainable for the player player given the decision x of all other players. Calls Game::NashGame::respond and obtains the std::unique_ptr to GRBModel of best response by player player. Then solves the model and returns the appropriate objective value.

Parameters

• sol – Output optimal response

• player – The input player’s id

• x – A std::vector of pure strategies (either for all players or all other players)

• fullvec – True if x contains the strategy for all players

Returns

The optimal objective value for the player player.

arma::vec computeQPObjectiveValues(const arma::vec &x, bool checkFeas = false) const

Computes players’ objective. Computes the objective value of each player in the Game::NashGame object.

Returns

An arma::vec with the objective values.

bool isSolved(const arma::vec &sol, unsigned int &violPlayer, arma::vec &violSol, double tol = 1e-4) const

Checks if the Nash game is solved.

Checks if the Nash game is solved, if not provides a proof of deviation

Parameters

• sol – The std::vector of pure strategies for the Nash Game

• violPlayer – Output index of the player with profitable deviation

• violSol – The output pure strategy for that player - which gives a profitable deviation

• tol – The deviation tolerance

NashGame &addDummy(unsigned int par = 0, int position = -1)

Add dummy variables (parameters) in a NashGame object. These are just zero columns that don’t feature in the problem anywhere. They are of importance only where the NashGame gets converted into an LCP and gets parametrized. Typically, they appear in the upper level objective in such a case.

Parameters

• par – Number of parameters

• position – Position of the parameters

Returns

NashGame &addLeadCons(const arma::vec &a, double b)

Adds Leader constraint to a NashGame object. In case common constraint to all followers is to be added (like a leader constraint in an MPEC), this function can be used. It adds a single constraint \( a^Tx \leq b\).

Parameters

• a – The constraint LHS

• b – The constraint RHS

Returns

A pointer to this

void write(const std::string &filename, bool append = true, bool KKT = false) const

Writes the Nash Game sum up to a file.

Parameters

• filename – The filename

• append – Should the method append to the file?

• KKT – True if the KKT needs to be included

void save(const std::string &filename, bool erase = true) const

Saves the Game::NashGame object in a loadable file.

long int load(const std::string &filename, long int pos = 0)

Loads the Game::NashGame object stored in a file.

Loads the NashGame object stored in a file. Before calling this function, use the constructor NashGame::NashGame(GRBEnv *Env) to initialize. Loads the NashGame object stored in a file. Before calling this function, use the constructor NashGame::NashGame(GRBEnv *Env) to initialize.

Example usage:

int main()
{
        GRBEnv Env;
        Game::NashGame N(&Env);
        N.load("./dat/Ndata.dat");
        std::cout<<N<<'\n';
        return 0;
}

Parameters

• filename – The filename

• pos – The start writing position

Returns

The end position

Private Functions

void setPositions()

Stores the position of each players’ primal and dual variables. Also allocates Leader’s position appropriately. The ordering is according to the columns of the following image.

Private Members

GRBEnv *Env = nullptr

A pointer to the Gurobi Environment.

arma::sp_mat LeaderConstraints

Upper level leader constraints LHS.

arma::vec LeaderConstraintsRHS

Upper level leader constraints RHS.

unsigned int NumPlayers

Number of players in the Nash Game.

VariableBounds Bounds

BoundsX on primal variables.

std::vector<std::shared_ptr<MathOpt::MP_Param>> Players

The QP that each player solves.

arma::sp_mat MarketClearing

Market clearing constraints.

arma::vec MCRHS

RHS to the Market Clearing constraints.

std::vector<unsigned int> PrimalPosition

In the vector of variables of all players, which position does the variable corresponding to this player starts.

std::vector<unsigned int> DualPosition

In the vector of variables of all players, which position do the DUAL variable corresponding to this player starts.

unsigned int MC_DualPosition = {}

Manages the position of Market clearing constraints’ duals.

unsigned int LeaderPosition = {}

Manages the position of where the leader’s variables start.

unsigned int numLeaderVar

Manages the position of where the leader’s variables start. These many variables will not have a matching complementary equations.

Friends

inline friend std::ostream &operator<<(std::ostream &os, const NashGame &N)

EPEC

class EPEC : public Game::AbstractGame<Data::EPEC::DataObject>

Class to handle a Nash game between leaders of Stackelberg games.

Subclassed by Models::EPEC::EPEC

Public Functions

inline EPEC(GRBEnv *env)

The standard constructor. Initialize an empty instance.

Parameters

env – The Gurobi environment pointer.

void finalize()

Finalizes the creation of a Game::EPEC object.

Performs a bunch of job after all data for a Game::EPEC object are given, namely. Models::EPEC::computeLeaderLocations - Adds the required dummy variables to each leader’s problem so that a game among the leaders can be defined. Calls Game::EPEC::addDummyLead

• Makes the market clearing constraint in each country. Calls

virtual void findNashEq() override

Computes Nash equilibrium using the Algorithm set in Game::EPEC::Algorithm. Checks the value of Game::EPEC::Algorithm and delegates the task to appropriate Algorithm wrappers.

virtual bool isSolved(double tol = 1e-5) const override

Call the delegated Algorithm method and return true if there exist a feasible equilibrium.

Parameters

tol – A numerical tolerance

Returns

True if the incumbent solution is an equilibrium

virtual bool isPureStrategy(double tol = 1e-5) const override

Call the delegated Algorithm method and return true if the equilibrium is pure.

Parameters

tol – A numerical tolerance

Returns

True if the incumbent equilibrium is pure

std::unique_ptr<GRBModel> bestResponseProgram(const unsigned int i, const arma::vec &x, MathOpt::PolyLCP *customLCP = nullptr) const

Given a player id i, the incumbent solution x (and optionally a custom player LCP customLCP), this method returns the model corresponding to the best response of i given the other players’ decisions in x.

Parameters

• i – The player id

• x – The incumbent solution

• customLCP – An optional parameter with a custom LCP

Returns

A pointer to the (solved) Gurobi model for the best response

double bestResponse(arma::vec &sol, unsigned int player, const arma::vec &x, const arma::vec &prevDev = {}, MathOpt::PolyLCP *customLCP = nullptr) const

Returns the best-response value for the player player given the decision x of all other players.

Calls Game::EPEC::respond and obtains the std::unique_ptr to GRBModel of best response by player player. Then solves the model and returns the appropriate objective value.

Parameters

• sol – The optimal response for player

• player – The player id

• x – The solution vector

• prevDev – An optional previous deviation encountered. This is useful to normalize any unbounded best response

• customLCP – An optional pointer to a custom player LCP.

Returns

The optimal objective value for the player player.

inline const arma::vec getX() const

Getter for the incumbent solution (x)

Returns

The incumbent x

inline const arma::vec getZ() const

Getter for the incumbent solution (z)

Returns

The incumbent z

void setAlgorithm(Data::EPEC::Algorithms algorithm)

Decides the Algorithm to be used for solving the given instance of the problem. The choice of algorithms are documented in Game::EPECalgorithm.

Parameters

algorithm – The input algorithm

void setRecoverStrategy(Data::EPEC::RecoverStrategy strategy)

Decides the Algorithm to be used for recovering a PNE out of the InnerApproximation procedure.

Parameters

strategy – Input ecovery strategy

void setBranchingStrategy(Data::EPEC::BranchingStrategy strategy)

Sets the branching strategy for the CutAndPlay.

Parameters

strategy – The input strategy

inline void setAggressiveness(unsigned int a)

inline void setAddPolyMethod(Data::LCP::PolyhedraStrategy add)

Set the Data::LCP::PolyhedraStrategy for the inner approximation.

unsigned int getPositionLeadFoll(unsigned int i, unsigned int j) const

Gets the position of the j-th variable in the i-th leader Querying Game::EPEC::LCPModel for x[return-value] variable gives the appropriate variable.

Parameters

• i – Leader number

• j – Follower number

Returns

The queried position

unsigned int getPositionLeadLead(unsigned int i, unsigned int j) const

Gets the position of the j-th Follower variable in the i-th leader Querying Game::EPEC::LCPModel for x[return-value] variable gives the appropriate variable.

Parameters

• i – Leader number

• j – Follower number

Returns

The queried position

double getValLeadFoll(unsigned int i, unsigned int j) const

Gets the value of the j-th variable in i-th leader.

Parameters

• i – Leader number

• j – Follower number

Returns

The queried position

double getValLeadLead(unsigned int i, unsigned int j) const

Gets the value of the j-th non-follower variable in i-th leader.

Parameters

• i – Leader number

• j – Follower number

Returns

The queried position

double getValProbab(unsigned int i, unsigned int k)

Returns the probability associated with the k -th polyhedron of the i -th leader.

Parameters

• i – Leader index

• k – The polyhedron index

Returns

The queried attribute

double getValLeadFollPoly(unsigned int i, unsigned int j, unsigned int k, double tol = 1e-5) const

For the i -th leader, gets the k -th pure strategy at position j.

Parameters

• i – The leader index

• j – The position index

• k – The pure strategy index

• tol – A numerical tolerance

Returns

The queried attribute

double getValLeadLeadPoly(unsigned int i, unsigned int j, unsigned int k, double tol = 1e-5) const

For the i -th leader, gets the k -th pure strategy at leader position j.

Parameters

• i – The leader index

• j – The position index

• k – The pure strategy index

• tol – A numerical tolerance

Returns

The queried attribute

std::vector<unsigned int> mixedStrategyPoly(unsigned int i, double tol = 1e-5) const

Returns the indices of polyhedra feasible for the leader, from which strategies are played with probability greater than the tolerance.

Parameters

• i – Leader index

• tol – Tolerance

Returns

The queried attribute

inline const MathOpt::LCP &getLCPDescription() const

Get the Game::LCP object solved in the last iteration either to solve the problem or to prove non-existence of Nash equilibrium. Object is returned using constant reference.

inline const GRBModel &getLCPModel() const

Get the GRBModel solved in the last iteration to solve the problem or to prove non-existence of Nash equilibrium. Object is returned using constant reference.

inline void writeLCPModel(const std::string &filename) const

Writes the GRBModel solved in the last iteration to solve the problem or to prove non-existence of Nash equilibrium to a file.

void getXWithoutHull(const arma::vec &x, arma::vec &xWithoutHull) const

Given the the solution x, the method returns in xWithoutHull the x vector without the convex-hull’s variables. Also, no MC variables are included.

Parameters

• x – The EPEC’s solution

• xWithoutHull – The output solution without convex hull variables

void getXofI(const arma::vec &x, const unsigned int &i, arma::vec &xOfI, bool hull = false) const

Given the player id i and the solution x, the method returns in xWithoutHull the x vector for the given player, with the convex-hull’s variables in case hull is false. Also, no MC variables are included.

Parameters

• x – The EPEC’s solution

• i – The player id

• xOfI – Output solution vector for i

• hull – True if convex-hull variables need to be included in the output

void setWelfareObjective(bool linear, bool quadratic)

Given the object Game::EPEC::LCPModel, this method sets its objective to the social welfare. In specific, we can decide whether to include or not the linear or quadratic part of the welfare

Parameters

• linear – True if the linear part is to be included, false otherwise.

• quadratic – True if the quadratic part is to be included, false otherwise.

Protected Functions

bool warmstart(const arma::vec &x)

Warmstarts EPEC with a solution.

Warmstart the solution with x.

Todo:

Complete this implementation

Parameters

x – The warmstart solution

Returns

True if the warmstart was successful

virtual void makeObjectivePlayer(const unsigned int i, MathOpt::QP_Objective &QP_obj) = 0

Empty function - optionally re-implementable in derived class.

Parameters

• i – The player id

• QP_obj – The QP_object with the objective

virtual void preFinalize() = 0

Empty function - optionally re-implementable in derived class.

This function can be optionally implemented by the derived class. Code in this class will be run before calling Game::EPEC::finalize().

virtual void postFinalize() = 0

Empty function - optionally re-implementable in derived class.

This function can be optionally implemented by the derived class. Code in this class will be run after calling Game::EPEC::finalize().

virtual void updateLocations() = 0

Empty function - optionally re-implementable in derived class.

If any location tracking system is implemented, that can be called from in here.

inline virtual void makeMCConstraints(arma::sp_mat &MC, arma::vec &RHS) const

Empty function - optionally re-implementable in derived class.

Builds the Market Clearing constraints

Parameters

• MC – MC constraints matrix

• RHS – RHS for the constraints

Protected Attributes

std::vector<std::shared_ptr<Game::NashGame>> PlayersLowerLevels = {}

The lower level Nash Games among the followers.

std::vector<std::shared_ptr<MathOpt::LCP>> PlayersLCP = {}

The LCP of each leader, encompassing both Stackelberg and low-level Nash games.

std::vector<std::shared_ptr<MathOpt::QP_Param>> PlayersQP = {}

The QP corresponding to each player.

std::vector<std::shared_ptr<MathOpt::QP_Objective>> LeaderObjective = {}

Objective of each leader.

std::vector<std::shared_ptr<MathOpt::QP_Objective>> LeaderObjectiveConvexHull = {}

Objective of each leader, given the convex hull computation.

std::unique_ptr<Game::NashGame> TheNashGame

The EPEC nash game.

std::vector<unsigned int> LeaderLocations = {}

Location of each leader Number of variables in the current player, including any number of convex hull variables at the current moment. The used, i.e., the inheritor of Game::EPEC has the responsibility to keep this correct by implementing an override of Game::EPEC::updateLocations.

std::vector<const unsigned int*> LocEnds = {}

The ending locations for the leaders’ variables.

std::vector<unsigned int> ConvexHullVariables = {}

Number of convex hull variables for each leader.

unsigned int numMCVariables = {0}

Number of market clearning variables.

bool Finalized = {false}

A flag controlling if the EPEC was finalized.

arma::vec SolutionZ

Solution equation values.

arma::vec SolutionX

Solution variable values.

Private Functions

void addDummyLead(unsigned int i)

Add Dummy variables for the leaders.

Adds dummy variables to the leader of an EPEC - useful after computing the convex hull.

Parameters

i – The leader id to whom dummy variables should be added

void makePlayerQP(unsigned int i)

Makes the MathOpt::QP_Param corresponding to the i-th country.

• First gets the Game::LCP object from Game::EPEC::PlayersLowerLevels and makes a MathOpt::QP_Param with this LCP as the lower level

• This is achieved by calling LCP::makeQP and using the objective value object in Game::EPEC::LeaderObjective

• Finally the locations are updated owing to the complete convex hull calculated during the call to LCP::makeQP

Note

Overloaded as Models::EPEC::makePlayerQP()

Parameters

i – The player’s id

void makePlayersQPs()

Makes the MathOpt::QP_Param for all the countries. Calls are made to Models::EPEC::makePlayerQP(const unsigned int i) for each valid player id.

void makeTheLCP()

Formulates the LCP to compute an equilibrium. In this LCP, each player’s feasible region is given by the PlayersQP associated entry. If the QP stems from a full enumeration, for instance, the solution will be exact.

void computeLeaderLocations(unsigned int addSpaceForMC = 0)

Assigns the values to LeaderLocations to each player.

Parameters

addSpaceForMC – contains the number of Market Clearing variables

void getXMinusI(const arma::vec &x, const unsigned int &i, arma::vec &xMinusI) const

Given a solution in x, computes the other players’ solution x minus i in xMinusI.

Parameters

• x – The incumbent solution

• i – The player id

• xMinusI – The output strategy

bool computeNashEq(bool pureNE, double localTimeLimit, bool check, bool linearWelfare, bool quadraticWelfare)

Given that Game::EPEC::PlayersQP are all filled with a each country’s MathOpt::QP_Param problem (either exact or approximate), computes the Nash equilibrium. pureNE checks for pure Nash Equilibrium. It does not work with EPEC::Algorithms::CutAndPlay localTimeLimit sets the timelimit for the solver. a negative value is infinite time check If true, the method calls the isSolved() method related to the active algorithm EPEC::Algorithms linearWelfare If true, the objective of the resulting LCP includes the sum of the linear objectives for the players quadraticWelfare If true, the objective of the resulting LCP includes the sum of the quadratic objectives for the players

Returns

true if a Nash equilibrium is found

Private Members

std::shared_ptr<Algorithms::EPEC::PolyBase> Algorithm = {}

The incumbent algorithm used to solve the instance.

std::vector<unsigned int> SizesWithoutHull = {}

Size of leaders’ variables without the convex hull variables.

std::unique_ptr<MathOpt::LCP> TheLCP

The EPEC nash game written as an LCP.

std::unique_ptr<GRBModel> LCPModel

A Gurobi mode object of the LCP form of EPEC.

std::unique_ptr<GRBModel> LCPModelBase

A Gurobi mode object of the LCP form of EPEC. If we are searching for a pure NE, the LCP which is indifferent to pure or mixed NE is stored in this object.

Friends

friend class Algorithms::EPEC::PolyBase

friend class Algorithms::EPEC::InnerApproximation

friend class Algorithms::EPEC::CutAndPlay

friend class Algorithms::EPEC::CombinatorialPNE

friend class Algorithms::EPEC::FullEnumeration

IPG

class IPG : public Game::AbstractGame<Data::IPG::DataObject>

This class handles Integer Programming Games (IPG), namely multiple agents solving an integer programming game.

Subclassed by Models::IPG::IPG

Public Functions

void finalize()

This methods finalizes the model by disabling any edits to the number of players. The proper object (for instance, the ones counting players variables) are initialized with the right values.

inline IPG(GRBEnv *env)

Standard initializer.

Parameters

env – A pointer to the Gurobi Environment

IPG(GRBEnv *env, std::vector<std::shared_ptr<MathOpt::IP_Param>> players)

This constructors initializes the integer programming game with the Gurobi environment env and the vector of shared pointers to the IP_Params in players.

Parameters

• env – A pointer to the Gurobi Environment

• players – A vector containing the pointers to the IP param for each player

• env – Pointer to the Gurobi environment

• players – The MathOpt::IP_Param for the players

virtual void findNashEq() override

The main method to start the solving process.

virtual bool isSolved(double tol = 1e-5) const override

Return a bool true if the strategies are all pure, for any player.

virtual bool isPureStrategy(double tol = 1e-5) const override

Return a bool indicating whether the equilibrium is a pure strategy.

inline std::vector<arma::vec> getX() const

Gets the X in the incumbent solution.

Returns

A const vector copy of X.

inline double getSocialWelfare() const

inline ZEROStatistics<Data::IPG::DataObject> getStatistics() const

Get the EPECStatistics object for the current instance.

inline void setAlgorithm(Data::IPG::Algorithms algorithm)

Sets the Data::IPG::Algorithms for the solution process.

Parameters

algorithm – An enum from Data::IPG::Algorithms

inline void setPresolve(bool value)

Sets the Data::IPG::Presolve for the solution process.

Parameters

value – A boolean for Data::IPG::Presolve

inline void setLCPAlgorithm(const Data::LCP::Algorithms algo)

Sets the Data::LCP::Algorithms for the LCP solution process.

Parameters

algo – An enum from Data::LCP::Algorithms

inline void setGameObjective(const Data::IPG::Objectives obj)

Sets the Data::IPG::Objectives for the LCP objective.

Parameters

obj – An enum from Data::IPG::Objectives

inline void setCutsAggressiveness(const Data::IPG::CutsAggressiveness aggressiveness)

Sets the Data::IPG::CutsAggressiveness for the cut aggressiveness in Algorithms::IPG::CutAndPlay.

Parameters

aggressiveness – An enum from Data::IPG::CutsAggressiveness

Protected Functions

virtual void preFinalize() = 0

Virtual (empty) method. Can be implemented by a derived class.

virtual void postFinalize() = 0

Virtual (empty) method. Can be implemented by a derived class.

Protected Attributes

std::vector<std::shared_ptr<MathOpt::IP_Param>> PlayersIP = {}

The Integer Programs associated to each player.

std::vector<unsigned int> PlayerVariables = {}

The number of variables for each player.

bool Finalized = {false}

std::vector<arma::vec> Solution

Solution variable values, for each player.

double SocialWelfare

SocialWelfare associated to the incumbent solution.

Private Members

std::shared_ptr<Algorithms::IPG::Algorithm> Algorithm = {}

The Algorithm’s instance.

Friends

friend class Algorithms::IPG::Algorithm

friend class Algorithms::IPG::CutAndPlay

friend class Algorithms::IPG::ZERORegrets